Intro Kinetics
Kinetics
Screencast will be up later today (Saturday, 4/18)General Stuff:
- Reactions (almost always) require collisions.
- Increased temperature increases the speed of the molecules, and therefore the number of collisions and the rate of the reaction.
- Increasing concentration also increases the rate (especially if collisions are required: more molecules means higher probability of collisions).
- A minimal temperature may be required to start the reaction.
Remember the rules for energy and bond formation:
Forming bonds releases energy to the surroundings (raises temperature).
Breaking bonds requires input energy from the surroundings (lowers temp).
The stronger the bond, the more energy required to break it, or, the more energy is released when it is formed.
Strong bonds means low energy state means stable molecule; but weak bonds means high energy state and less stable. Generally, forming lower-energy, more stable molecules is favored. However, getting between two fairly stable states may require getting over an energy "hump," known as the Activation Energy.
The magnitude of the activation energy generally determines how fast a reaction can proceed.
Measuring reaction rate:
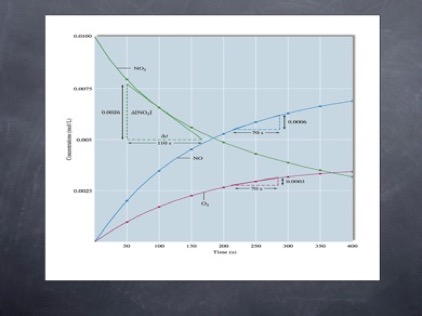
The rate of the reaction, for example, at high temperature, Nitrogen dioxide decomposes into Nitric oxide and oxygen. (It is an endothermic process....I wonder if you can guess why?) The rate of the reaction 2NO2 ⇄ 2NO +O2 will be given as the change in the concentration of NO2 over change in time
We also could look at any of the components...but NO2 is brown, and is easy to quantify). If we wanted to know the change in any of the others, we could predict it. It is probably obvious to all that the rate for the accumulation of NO will be the same in magnitude, but opposite sign, as the rate for consumption of NO2. That is, the slope of the red line at some time will be negative, while that of the blue will be positive at the same time. But they will have the same absolute value. However, what about the rate for O2? It is obvious from the stoichiometry that we are only going to make half as much O2 as we will NO. Therefore the rate of production of NO is 2x the rate of production of O2. So the rate of consumption of NO2 will be equal to the rate of production of NO and equal to twice the production of O2. The easiest way to do it is to just take the coefficient from each term take the inverse. That is, if the coefficient in the equation is “2,” it becomes a 1/2 in the rate expression. Or, we could multiply through by two. Write out the rate expression for each term.
The equation form of this statement is the "rate expression." You just track the one that is easiest.
The units for this are M/s (mole per liter per second).
The minus sign when considering is because the change in concentration of NO2 is negative, and we want to report a positive rate. We can plot concentration on the Y axis and the time on the X and we would get a curve looking like this:
Maybe this one is easier to read
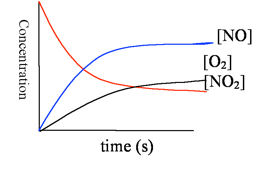
This shows that the concentration of the reactant drops over time, while that of the products increases. Note that the reactant never goes completely away. Like many spontaneous reactions, this does not go to completion, but rather reaches equilibrium. We describe the rate in three ways.
Measuring rate 2:
Once we decide which one we will measure, we have to decide exactly how to measure rate. We can calculate the average rate over some time, say, 50 seconds. We do this by measuring the amount of NO2 at 100 seconds, for example, and subtracting from that the amount of NO2 present at 50 seconds, then dividing by 50 seconds (the change in time). This would give us the average rate for that 50 second period. But, it is obvious that the rate changes over that 50-second period. It is faster in the beginning and slower at the end.
We could try to take the change in concentration over a really small interval. We could then find the slope of the line at one instant. That is the “instantaneous rate.” For those of you doing any calculus, you may realize that this is the first derivative of the equation, the slope of a tangent to the line or dy/dx as dx goes to zero. For the rest of you, the simple way to think of it is to imagine drawing a straight line that just kisses up to the curve. The slope of that line is the instantaneous rate.
The third way we talk about the rate is at the instant the reaction begins. That is known as the initial rate. In practice, this often is the easiest thing to measure.
Rate Laws:
Rate Laws come in two varieties: the differential rate law, which tells you the rate as a function of concentration of Reactant. and the integrated rate law, which tells you the concentration of reactant as a function of time.
Both need to be determined from experiment. You cannot predict the rate law without measuring it.
The general form of the rate law is
where "n" is the "order" of the reaction with respect to the reactant.

Determining "order"
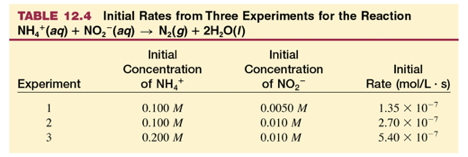
w

