Non-Ideal Gas
Ideal Gas Assumption:
As you know, we made two assumptions when we derived the Ideal Gas Law, PV=nRT.
Here is a link to the University of Colorado demo I was using.
These assumptions are not literally true. But, we get away with it as long as the molecules are moving fast enough (higher temp) that they don't stick and far enough apart (higher temp and lower pressure) that they take up a small amount of volume.
We can correct if we know how much volume the particles really do take up and how stick the particles are. Both of these will be different for each gas.
Johannes Diderik van der Waals was molecular physicist in the 19th and 20th century who won the Nobel Prize for Physics in 1910. He studied how molecules interact. We will return to him later when we address why, exactly, molecules might be "sticky" in the first place. Why isn't everything a gas? For now, we will look at how his work affected how we view gases. He was able to determine both how stick a particular molecule is and how much volume it occupies. These constants, called "a" and "b," are presented in a table below for a few gases. "a" is the stickiness factor, as I call it. "b" is the volume occupied by a particle of that gas.
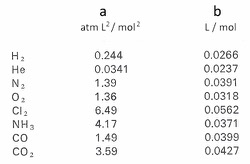
Let's look at how we use them:
This is pretty straightforward. The actual volume available to the particles as they move around is not that of the empty container. A flask might say it has a volume of 2.00L, but the more gas particles you put in it the less space each one has to move around.
In the lab, we found that about 0.1 mol of liquid dustoff has a volume of about 8mL (0.008L) and expands to about 2.4L of gas at room temperature and normal atmospheric pressure. So, our idea that we don't really need to account for the volume of particles most of the time is supported. The condensed particles took up only `0.008/2.4` or only 0.3% of the volume. From this, we could conclude that 1 mole of dustoff would take up about 0.08L. If you look up the Van der Waals constant for 1,1 difluoroethane, you will find it is about 0.07L/mol. So, we were really close.
How do we use this? Well, the volume actually available to each particle is the nominal volume of the container minus the volume of the particles themselves, which is nb: the number of moles of gas times the volume occupied by a mole of particles.
`V_{actual}=V_{nominal}-nb`
Stickiness factor
Well, that's what I call it anyway. Think of it like this: if two particles collide and stick, they behave as one particle for as long as they are stuck together. That effectively drops the number of particles and therefore drops the pressure (fewer separate particles mean fewer collisions with the container wall). The particles all have the same average kinetic energy. But, if two particles are stuck together, they have ¼ the velocity (KE-1/2mv2).
To figure out how many particles are stuck together, we have to account for how stick the particles are (different for each gas, that's the constant "a") and how often they collide (which depends on how dense the particles are…how many mol/L). It actually depends on mol2/L2 because of some probability rules I'm not going to go into.
So, the pressure we measure is usually lower than what the pressure should be. We substitute:
`P+an^2/V^2`
The full gas law becomes:
`(P+an^2/V^2)(V-nb)=nRT`
You will not have to use this equation to carry out calculations. But you will need to know what each correction does, why we don't need it most of the time, the conditions under which we might need it and, conceptually, how the constants correct for the non-ideal behavior.
As you know, we made two assumptions when we derived the Ideal Gas Law, PV=nRT.
- The particles occupy no volume
- The particles do not interact when they collide (stick together)
Here is a link to the University of Colorado demo I was using.
These assumptions are not literally true. But, we get away with it as long as the molecules are moving fast enough (higher temp) that they don't stick and far enough apart (higher temp and lower pressure) that they take up a small amount of volume.
We can correct if we know how much volume the particles really do take up and how stick the particles are. Both of these will be different for each gas.
Van der Waals Constants:
Johannes Diderik van der Waals was molecular physicist in the 19th and 20th century who won the Nobel Prize for Physics in 1910. He studied how molecules interact. We will return to him later when we address why, exactly, molecules might be "sticky" in the first place. Why isn't everything a gas? For now, we will look at how his work affected how we view gases. He was able to determine both how stick a particular molecule is and how much volume it occupies. These constants, called "a" and "b," are presented in a table below for a few gases. "a" is the stickiness factor, as I call it. "b" is the volume occupied by a particle of that gas.

Let's look at how we use them:
Volume of the particles
This is pretty straightforward. The actual volume available to the particles as they move around is not that of the empty container. A flask might say it has a volume of 2.00L, but the more gas particles you put in it the less space each one has to move around.
In the lab, we found that about 0.1 mol of liquid dustoff has a volume of about 8mL (0.008L) and expands to about 2.4L of gas at room temperature and normal atmospheric pressure. So, our idea that we don't really need to account for the volume of particles most of the time is supported. The condensed particles took up only `0.008/2.4` or only 0.3% of the volume. From this, we could conclude that 1 mole of dustoff would take up about 0.08L. If you look up the Van der Waals constant for 1,1 difluoroethane, you will find it is about 0.07L/mol. So, we were really close.
How do we use this? Well, the volume actually available to each particle is the nominal volume of the container minus the volume of the particles themselves, which is nb: the number of moles of gas times the volume occupied by a mole of particles.
`V_{actual}=V_{nominal}-nb`
Stickiness factor
Well, that's what I call it anyway. Think of it like this: if two particles collide and stick, they behave as one particle for as long as they are stuck together. That effectively drops the number of particles and therefore drops the pressure (fewer separate particles mean fewer collisions with the container wall). The particles all have the same average kinetic energy. But, if two particles are stuck together, they have ¼ the velocity (KE-1/2mv2).
To figure out how many particles are stuck together, we have to account for how stick the particles are (different for each gas, that's the constant "a") and how often they collide (which depends on how dense the particles are…how many mol/L). It actually depends on mol2/L2 because of some probability rules I'm not going to go into.
So, the pressure we measure is usually lower than what the pressure should be. We substitute:
`P+an^2/V^2`
The full gas law becomes:
`(P+an^2/V^2)(V-nb)=nRT`
You will not have to use this equation to carry out calculations. But you will need to know what each correction does, why we don't need it most of the time, the conditions under which we might need it and, conceptually, how the constants correct for the non-ideal behavior.
